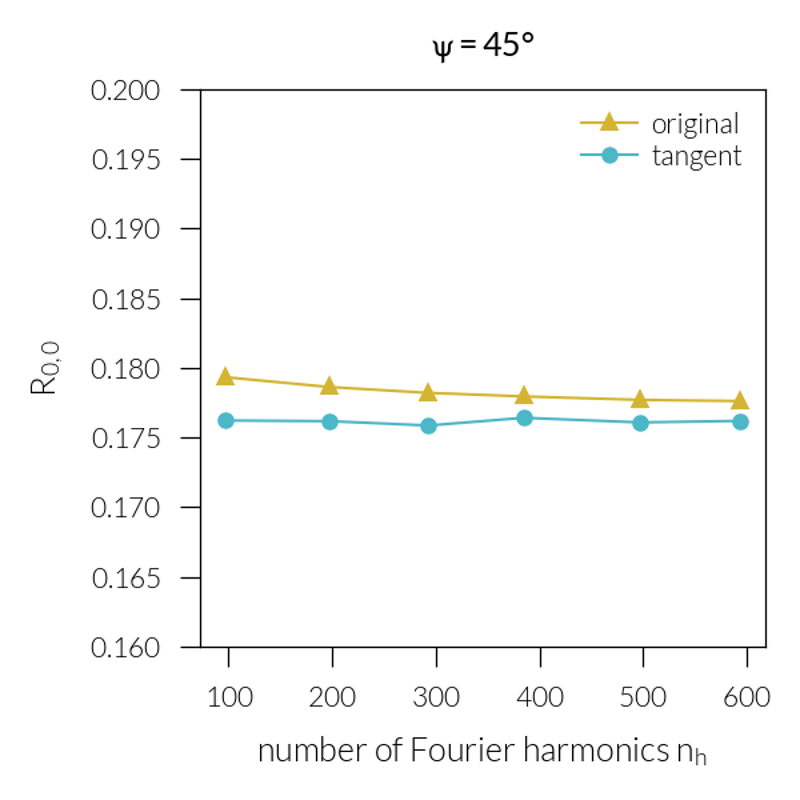
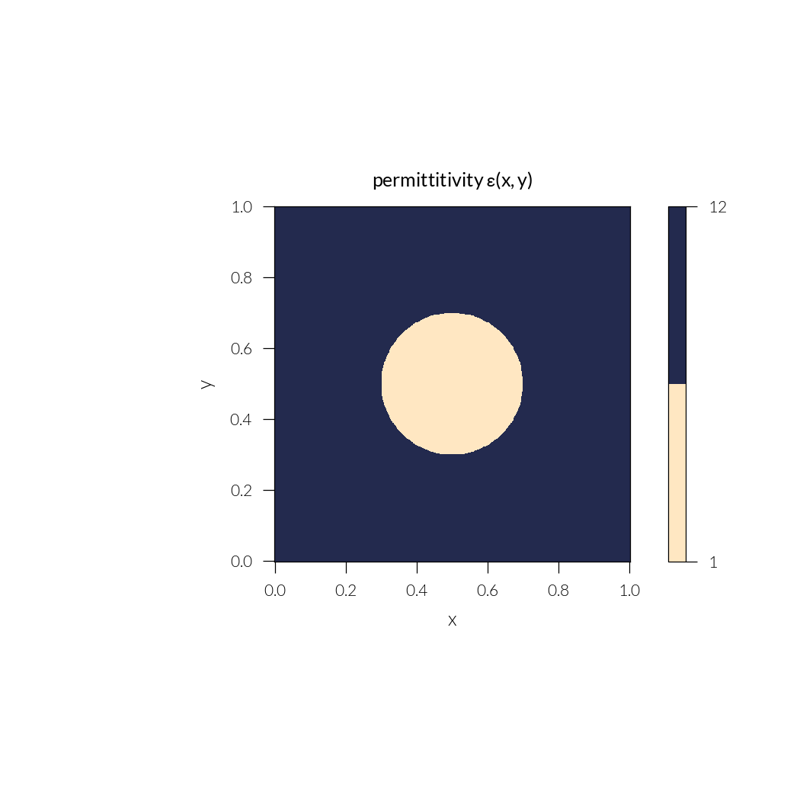
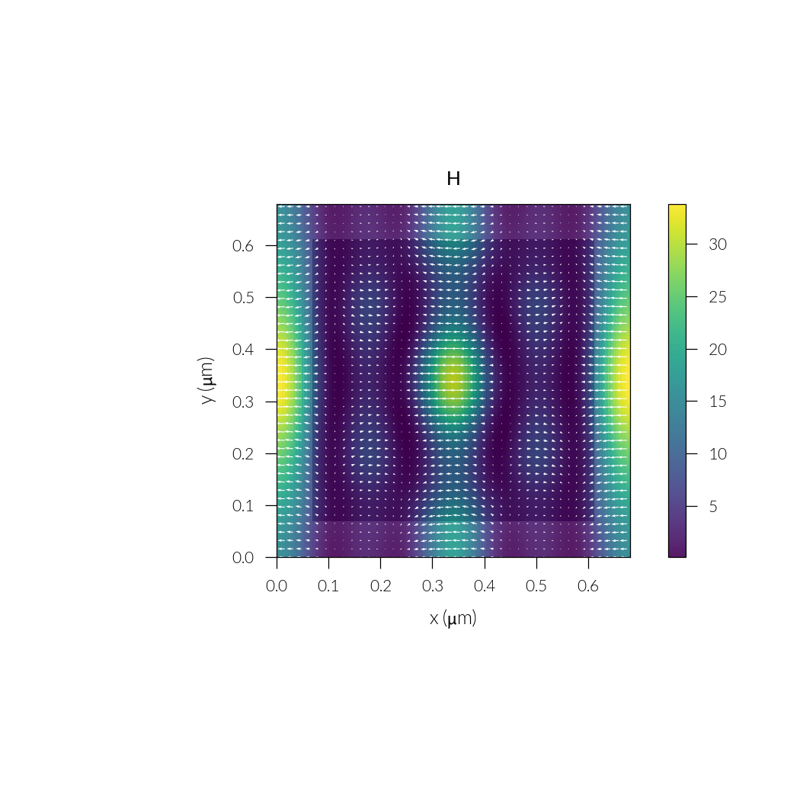
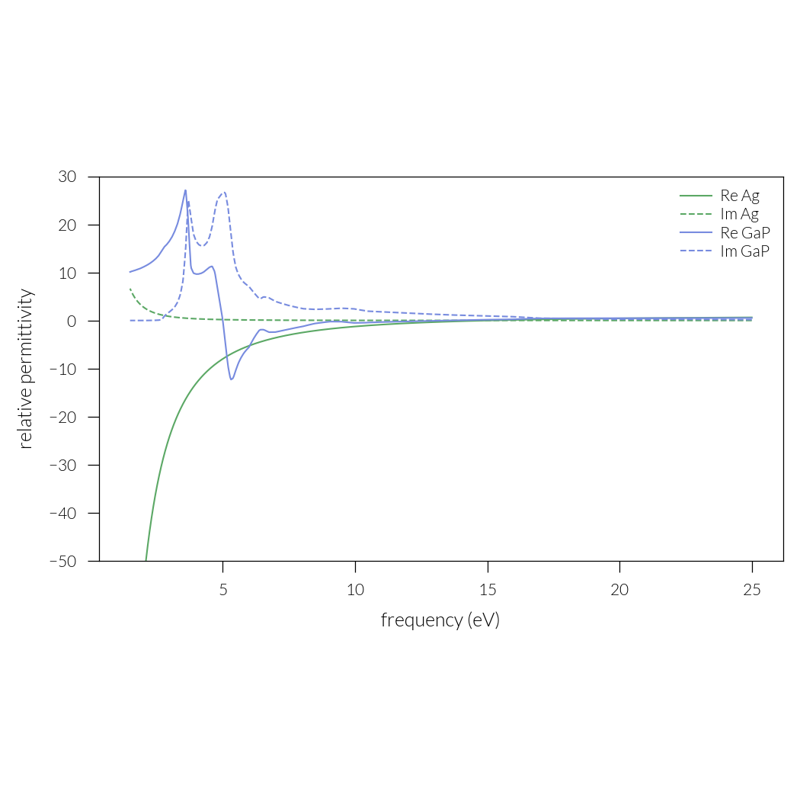
Simulation#

class nannos.Simulation(layers, excitation, nh=100, formulation='original')[source]#

Main simulation object.

Parameters:

layers (list) – A list of Layer objects.
excitation (PlaneWave) – A plane wave excitation .
nh (int) – Number of Fourier harmonics (the default is 100).
formulation (str) – Formulation type. (the default is 'original'). Available formulations are 'original', 'tangent', 'jones' and 'pol'.

build_matrix(layer)[source]#

Build the matrix for a given layer.

Parameters:: layer (int or Layer) – The layer to build the matrix for. If int, the layer is identified by its index.
Returns:: The layer with the computed matrix
Return type:: Layer

diffraction_efficiencies(orders=False, complex=False, return_dict=False)[source]#

Compute the diffraction efficiencies.

Parameters:

orders (bool) – If True, returns diffracted orders, else returns the sum of reflection and transmission for all propagating orders (the default is False).
complex (bool) – If True, return complex valued quantities corresponding to ampitude related coefficients. (the default is False).
return_dict (bool) – If True, return quantities as nested dictionaries with keys corresponding to diffraction orders. This works only if orders=True (the default is False).

Returns:

The reflection and transmission R and T.

Return type:

tuple

get_Efield_grid(layer_index, z=0, shape=None, component='all')[source]#

Retrieve the electric field in real space for a given layer.

Parameters:

layer_index (int) – The layer index
z (float, optional) – The z coordinate of the field, by default 0
shape (tuple, optional) – The shape of the output array, by default None
component (str, optional) – The component of the field, by default “all”. Must be one of “all”, “x”, “y”, “z”

Returns:

The electric field in real space. The shape of the array depends on the arguments.

Return type:

array

get_Hfield_grid(layer_index, z=0, shape=None, component='all')[source]#

Retrieve the magnetic field in real space for a given layer.

Parameters:

layer_index (int) – The layer index
z (float, optional) – The z coordinate of the field, by default 0
shape (tuple, optional) – The shape of the output array, by default None
component (str, optional) – The component of the field, by default “all”. Must be one of “all”, “x”, “y”, “z”

Returns:

The magnetic field in real space. The shape of the array depends on the arguments.

Return type:

array

get_S_matrix(indices=None)[source]#

Compute the scattering matrix.

Parameters:: indices (list) – Indices [i_first,i_last] of the first and last layer (the default is None). By default get the S matrix of the full stack.
Returns:: The scattering matrix [[S11, S12], [S21,S22]].
Return type:: list

get_epsilon(layer_id, axes=(0, 1))[source]#

Return the epsilon_zz component of the epsilon tensor.

Parameters:

layer_id (int or Layer) – The layer to get the epsilon from.
axes (tuple of int, optional) – The axes to return the epsilon for. Default is (0, 1).

Returns:

The epsilon_zz component of the epsilon tensor.

Return type:

array

get_field_fourier(layer_index, z=0)[source]#

Compute the fields in k-space for a given layer and z position.

Parameters:

layer_index (int) – Index of the layer
z (float or array) – The z position(s) at which to compute the fields

Returns:

fields_fourier – The fields in k-space for the given layer and z position(s)

Return type:

array

get_field_grid(layer_index, z=0, shape=None, field='all', component='all')[source]#

Retrieve the fields in real-space for a given layer.

Parameters:

layer_index (int) – The layer index
z (float, optional) – The z coordinate of the field, by default 0
shape (tuple, optional) – The shape of the output array, by default None
field (str, optional) – The field type, by default “all”. Must be one of “all”, “E” or “H”
component (str, optional) – The component of the field, by default “all”. Must be one of “all”, “x”, “y” or “z”

Returns:

The fields in real space. The shape of the array depends on the arguments.

Return type:

array

get_ifft(u, shape, axes=(0, 1))[source]#

Compute the inverse Fourier transform of an array u.

Parameters:

u (array) – The array to transform
shape (tuple) – The shape of the output array
axes (tuple) – The axes to transform over

Returns:

The inverse Fourier transformed array

Return type:

array

get_ifft_amplitudes(amplitudes, shape, axes=(0, 1))[source]#

Compute the inverse Fourier transform of the amplitudes in k-space.

Parameters:

amplitudes (array) – The amplitudes to transform
shape (tuple) – The shape of the output array
axes (tuple) – The axes to transform over

Returns:

The inverse Fourier transformed amplitudes

Return type:

array

get_layer(id)[source]#

Helper to get layer index and name.

Parameters:

id (int or str) – The index of the layer or its name.

Returns:

layer (nannos.Layer) – The layer object.
index (nannos.Layer) – The layer index in the stack.

get_order(A, order)[source]#

Return the element of A at the index corresponding to the order.

Parameters:

A (array like) – The array to index into
order (tuple or int) – The order to find the index of. If int, the second element of the tuple is assumed to be 0.

Returns:

The element at the index corresponding to the order in A

Return type:

element

get_order_index(order)[source]#

Return the index of the order (m,n) in the harmonics array.

Parameters:: order (tuple or int) – The order to find the index of. If int, the second element of the tuple is assumed to be 0.
Returns:: The index of the order in the harmonics array.
Return type:: int
Raises:: ValueError – If the order is not a tuple of two integers for bi-periodic gratings.

get_z_poynting_flux(layer, an, bn)[source]#

Compute the z-component of the Poynting vector.

Parameters:

layer (Layer) – The layer
an (array) – The amplitudes of the forward fields
bn (array) – The amplitudes of the backward fields

Returns:

forward (array) – The z-component of the Poynting vector of the forward fields
backward (array) – The z-component of the Poynting vector of the backward fields

get_z_stress_tensor_integral(layer_index, z=0)[source]#

Compute the z-component of the stress tensor integral for the given layer at a given z position.

Parameters:

layer_index (int) – The index of the layer
z (float) – The z position

Returns:

The x, y and z components of the stress tensor integral

Return type:

tuple

plot_structure(plotter=None, nper=(1, 1), dz=0.0, null_thickness=None, **kwargs)[source]#

Plot the structure.

Parameters:

plotter (function, optional) – Custom function to plot the structure. Signature should be plotter(simulation, nper, dz, null_thickness, **kwargs).
nper (tuple of int, optional) – Number of periods in the x and y direction.
dz (float, optional) – The distance of the structure from the z=0 plane.
null_thickness (float, optional) – The thickness of the null layers at the top and bottom of the structure.

Return type:

None

reset(param='all')[source]#

Reset some or all of the simulation.

Parameters:: param (str, optional) – The parameter to reset. If "S", the S matrix is reset. If "solve", the simulation is reset to unsolved state. If "all", both are reset. The default is "all".
Return type:: None

solve()[source]#

Solve the eigenproblem for all layers in the stack.

This method loops over all layers in the stack and calls the build_matrix and solve_eigenproblem methods for each layer. The solved layers are stored in the layers attribute of the simulation object.

Notes

This method is called automatically by the run method of the simulation object.