Elliptical holes

Convergence checks.

import matplotlib.pyplot as plt
import numpy as np

import nannos as nn

We will study the convergence on a benchmark case from [Schuster2007]. First we define the main function that performs the simulation.

def array_ellipse(nh, formulation, psi):
    wl = 500 + 1e-6  # avoid Wood-Rayleigh anomaly
    d = 1000
    Nx = 2**9
    Ny = 2**9
    lattice = nn.Lattice(([d, 0], [0, d]), discretization=(Nx, Ny))
    pw = nn.PlaneWave(wavelength=wl, angles=(0, 0, psi))
    epsgrid = lattice.ones() * (1.75 + 1.5j) ** 2
    ell = lattice.ellipse((0.5 * d, 0.5 * d), (1000 / 2, 500 / 2), rotate=45)
    epsgrid[ell] = 1

    sup = lattice.Layer("Superstrate", epsilon=1)
    sub = lattice.Layer("Substrate", epsilon=1.5**2)
    st = lattice.Layer("Structured", thickness=50)
    st.epsilon = epsgrid

    sim = nn.Simulation([sup, st, sub], pw, nh, formulation=formulation)
    order = (0, 0)
    R, T = sim.diffraction_efficiencies(orders=True)
    r = sim.get_order(R, order)
    return R, T, r, sim


#
# sim = array_ellipse(100, "original")
# lay = sim.get_layer("Structured")
# lay.plot()
# plt.show()

Perform the simulation for different formulations and number of retained harmonics:

NH = [100, 200, 300, 400, 500, 600]
formulations = ["original", "tangent"]


def run_convergence(psi):
    nhs = {f: [] for f in formulations}
    rs = {f: [] for f in formulations}

    for nh in NH:
        print("============================")
        print("number of harmonics = ", nh)
        print("============================")
        for formulation in formulations:
            Ri, Ti, r, sim = array_ellipse(nh, formulation=formulation, psi=psi)
            R = np.sum(Ri)
            T = np.sum(Ti)
            print("formulation = ", formulation)
            print("nh0 = ", nh)
            print("nh = ", sim.nh)
            print("r = ", r)
            print("R = ", R)
            print("T = ", T)
            print("R+T = ", R + T)
            print("-----------------")
            nhs[formulation].append(sim.nh)
            rs[formulation].append(r)

    return nhs, rs

Plot the results:

markers = {"original": "^", "tangent": "o"}
colors = {
    "original": "#d4b533",
    "tangent": "#4cb7c6",
}

plt.ion()

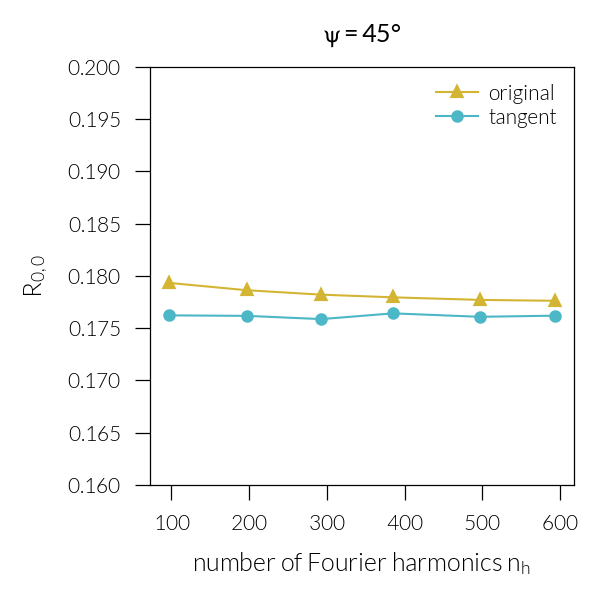
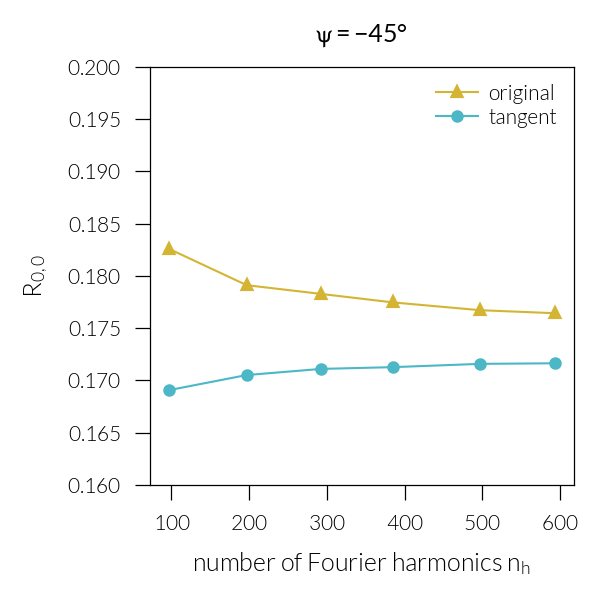
for psi in [45, -45]:
    nhs, rs = run_convergence(psi)
    plt.figure(figsize=(2, 2))

    for formulation in formulations:
        plt.plot(
            nhs[formulation],
            rs[formulation],
            "-",
            color=colors[formulation],
            marker=markers[formulation],
            label=formulation,
        )
        plt.pause(0.1)
    plt.legend()
    plt.xlabel("number of Fourier harmonics $n_h$")
    plt.ylabel("$R_{0,0}$")
    t = "" if psi == 45 else "-"
    plt.title(rf"$\psi = {t}45\degree$")
    plt.ylim(0.16, 0.2)
    plt.tight_layout()
    plt.show()

• 
• 

============================
number of harmonics =  100
============================
formulation =  original
nh0 =  100
nh =  97
r =  0.17932439123769872
R =  0.215150746939243
T =  0.4338385261002044
R+T =  0.6489892730394474
-----------------
/opt/conda/lib/python3.14/site-packages/autograd/wrap_util.py:38: SyntaxWarning: 'return' in a 'finally' block
  return f
formulation =  tangent
nh0 =  100
nh =  97
r =  0.1762160235083029
R =  0.2119104301374234
T =  0.4393625666893269
R+T =  0.6512729968267503
-----------------
============================
number of harmonics =  200
============================
formulation =  original
nh0 =  200
nh =  197
r =  0.17862181801800564
R =  0.21467135614446886
T =  0.4357577344352628
R+T =  0.6504290905797316
-----------------
formulation =  tangent
nh0 =  200
nh =  197
r =  0.17616788969044084
R =  0.21213490853620093
T =  0.44013107069634044
R+T =  0.6522659792325414
-----------------
============================
number of harmonics =  300
============================
formulation =  original
nh0 =  300
nh =  293
r =  0.17819846373023118
R =  0.21432898456661204
T =  0.43675889938964924
R+T =  0.6510878839562613
-----------------
formulation =  tangent
nh0 =  300
nh =  293
r =  0.17585848435853788
R =  0.21188982193127165
T =  0.4407413986576104
R+T =  0.652631220588882
-----------------
============================
number of harmonics =  400
============================
formulation =  original
nh0 =  400
nh =  385
r =  0.17794295536831056
R =  0.21413192473441922
T =  0.4373867488249516
R+T =  0.6515186735593708
-----------------
formulation =  tangent
nh0 =  400
nh =  385
r =  0.176407732255064
R =  0.21247042907870384
T =  0.4397829073376796
R+T =  0.6522533364163834
-----------------
============================
number of harmonics =  500
============================
formulation =  original
nh0 =  500
nh =  497
r =  0.17769663144135708
R =  0.21393385297317377
T =  0.43792851706935554
R+T =  0.6518623700425293
-----------------
formulation =  tangent
nh0 =  500
nh =  497
r =  0.17607882894831567
R =  0.2121936730970382
T =  0.44066791474916644
R+T =  0.6528615878462046
-----------------
============================
number of harmonics =  600
============================
formulation =  original
nh0 =  600
nh =  593
r =  0.17761068811836284
R =  0.21386973143079804
T =  0.4381744023749625
R+T =  0.6520441338057605
-----------------
formulation =  tangent
nh0 =  600
nh =  593
r =  0.17618672613291186
R =  0.21234017463895774
T =  0.4404056387350223
R+T =  0.6527458133739801
-----------------
============================
number of harmonics =  100
============================
formulation =  original
nh0 =  100
nh =  97
r =  0.18258253665287333
R =  0.2181789165421059
T =  0.4146478675652047
R+T =  0.6328267841073106
-----------------
formulation =  tangent
nh0 =  100
nh =  97
r =  0.16905807960477465
R =  0.20703150564147726
T =  0.4443842827674808
R+T =  0.6514157884089581
-----------------
============================
number of harmonics =  200
============================
formulation =  original
nh0 =  200
nh =  197
r =  0.17910497572918638
R =  0.2156715559542283
T =  0.4214226719302613
R+T =  0.6370942278844896
-----------------
formulation =  tangent
nh0 =  200
nh =  197
r =  0.17050332986430933
R =  0.2083975814321527
T =  0.44122222175197856
R+T =  0.6496198031841313
-----------------
============================
number of harmonics =  300
============================
formulation =  original
nh0 =  300
nh =  293
r =  0.17826595659553623
R =  0.2148941980208915
T =  0.42310259167465114
R+T =  0.6379967896955426
-----------------
formulation =  tangent
nh0 =  300
nh =  293
r =  0.17109234507590898
R =  0.2088494973206333
T =  0.43983055437586377
R+T =  0.648680051696497
-----------------
============================
number of harmonics =  400
============================
formulation =  original
nh0 =  400
nh =  385
r =  0.17745718861034127
R =  0.21428207178796826
T =  0.4248286708906074
R+T =  0.6391107426785756
-----------------
formulation =  tangent
nh0 =  400
nh =  385
r =  0.1712592537848026
R =  0.20903015319437807
T =  0.43930434079647007
R+T =  0.6483344939908482
-----------------
============================
number of harmonics =  500
============================
formulation =  original
nh0 =  500
nh =  497
r =  0.17671119584012301
R =  0.2137277006901238
T =  0.42635181241916936
R+T =  0.6400795131092931
-----------------
formulation =  tangent
nh0 =  500
nh =  497
r =  0.17157333390232027
R =  0.2093375103676635
T =  0.43871715418540946
R+T =  0.6480546645530729
-----------------
============================
number of harmonics =  600
============================
formulation =  original
nh0 =  600
nh =  593
r =  0.17642271922953728
R =  0.21347960227985674
T =  0.427157808785153
R+T =  0.6406374110650097
-----------------
formulation =  tangent
nh0 =  600
nh =  593
r =  0.17162950445599606
R =  0.20940691451349785
T =  0.4385434785407916
R+T =  0.6479503930542895
-----------------

Estimated memory usage: 3557 MB