Computing gradients

In this tutorial we will see how to compute gradients of quantities with respect to input values automatically.

import matplotlib.pyplot as plt

import nannos as nn

nn.set_backend("torch")
# nn.set_backend("autograd")
from nannos import grad

bk = nn.backend

Let’s define a function that will return the reflection coefficient for a metasurface:

def f(thickness):
    lattice = nn.Lattice(([1, 0], [0, 1]))
    sup = lattice.Layer("Superstrate")
    sub = lattice.Layer("Substrate", epsilon=2)
    ms = lattice.Layer("ms", thickness=thickness, epsilon=6)
    sim = nn.Simulation(
        [sup, ms, sub],
        nn.PlaneWave(1.5),
        nh=1,
    )
    R, T = sim.diffraction_efficiencies()
    return R


x = bk.array([0.3], dtype=bk.float64)
print(f(x))

tensor(0.0317, dtype=torch.float64)

We will compute the finite difference approximation of the gradient:

def first_finite_differences(f, x):
    eps = 1e-4
    return nn.backend.array(
        [(f(x + eps * v) - f(x - eps * v)) / (2 * eps) for v in nn.backend.eye(len(x))],
    )


df_fd = first_finite_differences(f, x)
print(df_fd)

tensor([-0.7177], dtype=torch.float64)

Automatic differentiation:

df = grad(f)
df_auto = df(x)
print(df_auto)

assert nn.backend.allclose(df_fd, df_auto, atol=1e-7)

tensor([-0.7177], dtype=torch.float64)

A random pattern:

import random

random.seed(2022)

discretization = 2**4, 2**4


def f(var):
    lattice = nn.Lattice(([1, 0], [0, 1]), discretization=discretization)
    xa = var.reshape(lattice.discretization)
    sup = lattice.Layer("Superstrate")
    sub = lattice.Layer("Substrate")
    ms = lattice.Layer("ms", 1)
    ms.epsilon = 9 + 1 * xa + 0j
    sim = nn.Simulation(
        [sup, ms, sub],
        nn.PlaneWave(1.5),
        nh=51,
    )
    R, T = sim.diffraction_efficiencies()
    return R


nvar = discretization[0] * discretization[1]
print(nvar)

xlist = [random.random() for _ in range(nvar)]
x = bk.array(xlist, dtype=bk.float64)

256

Finite differences:

t0 = nn.tic()
df_fd = first_finite_differences(f, x)
tfd = nn.toc(t0)

elapsed time 17.841123819351196s

Automatic differentiation:

df = grad(f)
t0 = nn.tic()
df_auto = df(x)
tauto = nn.toc(t0)


assert nn.backend.allclose(df_fd, df_auto, atol=1e-7)

print("speedup: ", tfd / tauto)

elapsed time 0.14763927459716797s
speedup:  120.84266783368106

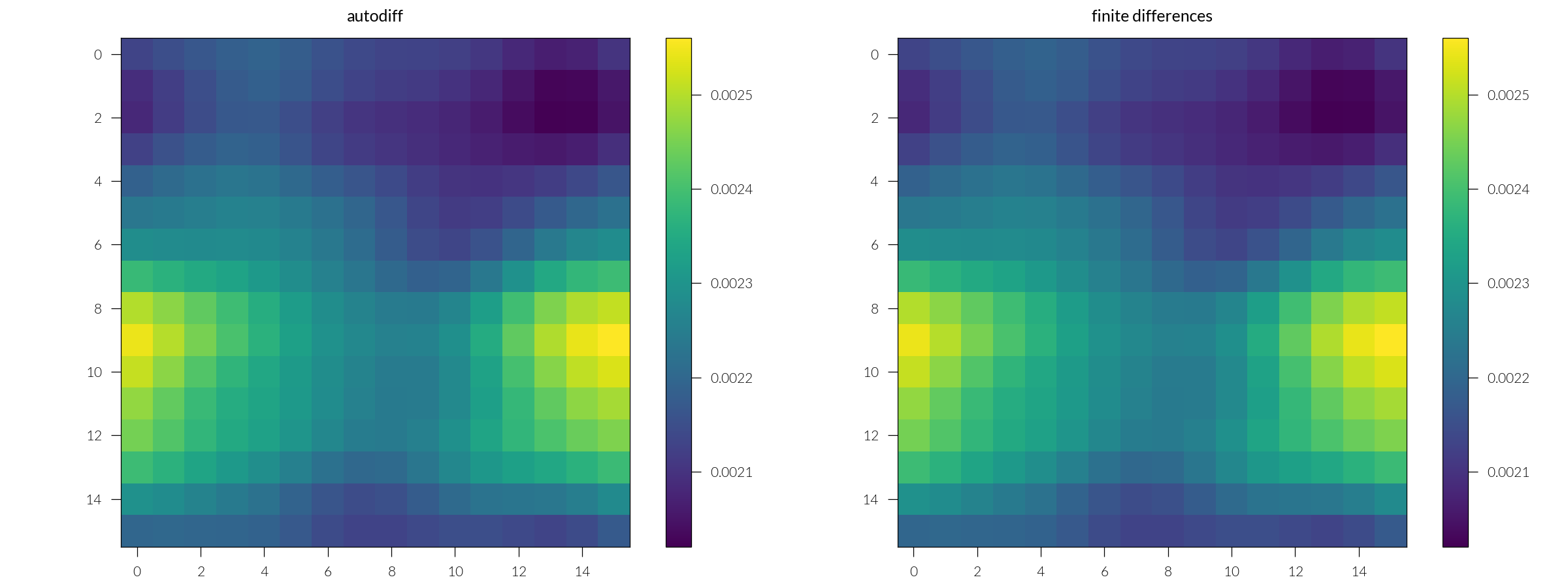
Plot gradients

fig, ax = plt.subplots(1, 2, figsize=(8, 3))
_ = ax[0].imshow(df_auto.reshape(*discretization).real)
plt.colorbar(_, ax=ax[0])
ax[0].set_title("autodiff")
_ = ax[1].imshow(df_fd.reshape(*discretization).real)
plt.colorbar(_, ax=ax[1])
ax[1].set_title("finite differences")
plt.tight_layout()


nn.set_backend("numpy")

Estimated memory usage: 544 MB